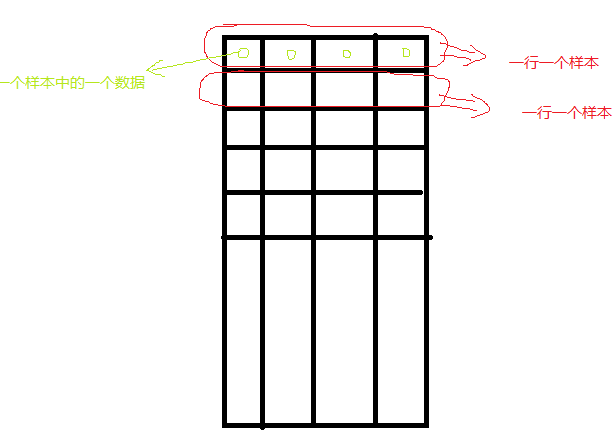
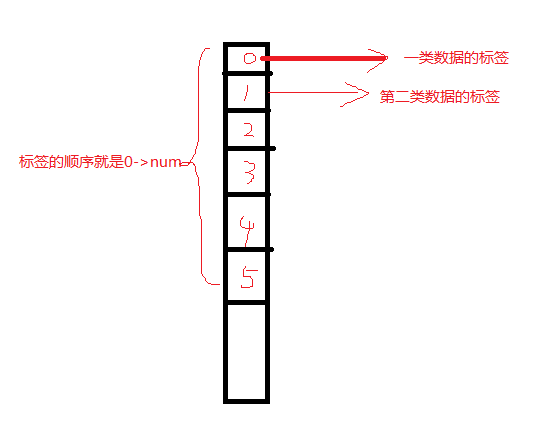
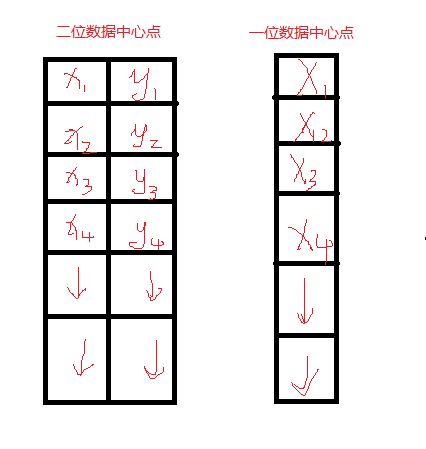
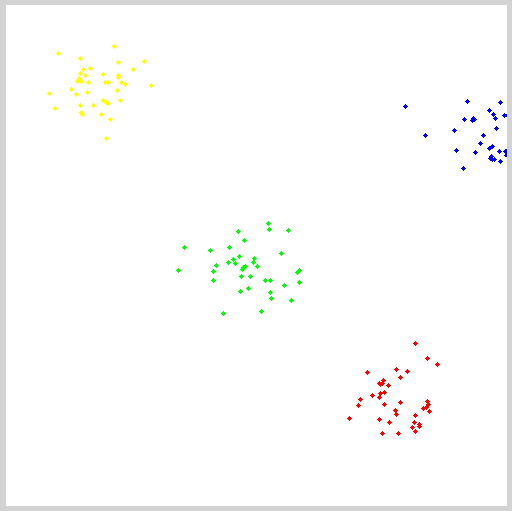
Written in the front: Before you wanted to classify the images, you saw the k-means algorithm. When you used it, you didn't understand the principle and didn't understand the rules. . . Obviously it finally failed. Then he read the book "Machine Learning" and he had a theoretical understanding of the k-means algorithm. Now he has practical understanding of the video by Jia Zhigang. K-means algorithm principle Note: Just as before, the core is someone else's. I'm just a porter of knowledge and added my own understanding. After the completion of the discovery of the theory part is the other ~ ~ no way this algorithm is too simple. . . K-means Meaning: Unsupervised clustering algorithm. Unsupervised: Without human intervention, a large number of things can be put directly into the algorithm and can be classified. Both SVM and neural network need to be trained in advance and then categorized. This is supervised learning. K-means and K-nearest neighbors are unsupervised learning. Clustering: Classifications that come together through a center, such as giving you a batch of data that divides you into three categories, that is, three centers. The meaning of these three centers represents three classes. K-means steps: From the above figure, we can see that A, B, C, D, E are five points in the figure. The gray point is our seed point, which is the point we use to find the point group. There are two seed points, so K=2. Then, K-Means' algorithm is as follows: Randomly take K (here K=2) seed points in the graph. Then find the distance to the K seed points for all the points in the graph. If the point Pi is closest to the seed point Si, then Pi belongs to the Si point group. (In the above figure, we can see that A, B belongs to the above seed point, C, D, E belongs to the seed point below the middle) Next, we want to move the seed point to the center of his "point group." (See the third step on the picture) Then repeat steps 2) and 3) until the seed points are not moved (we can see that the seed points above the fourth step in the figure aggregate A, B, C, and the seed points below converge D, E) . This algorithm is very simple, but there are some details I want to mention, I do not say the distance formula, everyone who has a junior high school graduation level should know how to count. I would like to focus on "the algorithm for the center of the point group." The algorithm for finding the center of the point group In general, you can use the average of the X/Y coordinates of each point simply to find the center point of the point group. However, here I would like to tell you the formula for the other three central points: Minkowski Distance Formula - λ can be any value, can be negative, it can be a positive number, or infinity. Euclidean Distance formula - that is, the first formula λ = 2 CityBlock Distance formula - that is, the first formula λ=1 The disadvantages of k-means: In K-means algorithm, K is given in advance, and the choice of this K value is very difficult to estimate. Many times, it is not known in advance how many categories a given data set should be divided into. This is also a deficiency of the K-means algorithm. In the K-means algorithm, it is first necessary to determine an initial partition based on the initial cluster center and then optimize the initial partition. The choice of the initial clustering center has a greater impact on the clustering results. Once the initial values ​​are not well selected, an effective clustering result may not be obtained. This has become a major problem in the K-means algorithm. From the K-means algorithm framework, it can be seen that the algorithm needs to continually adjust the sample classification and continuously calculate the adjusted new clustering center. Therefore, when the data volume is very large, the time overhead of the algorithm is very large. Opencv+K-means Nothing to write, because this k-means is relatively simple, the main thing is the application of function parameters only: Void RNG::fill(InputOutputArray mat, int distType, InputArray a, InputArray b, bool saturateRange=false ) This function fills the random number of the matrix mat. The random number generation method is determined by the parameter 2. If the type of the parameter 2 is RNG::UNIFORM, it means that a random number is generated with a uniform distribution. If it is RNG::NORMAL, it means that Gaussian distribution of random numbers. The corresponding parameters 3 and 4 are the parameters of the above two random number generation models. For example, if the random number production model is uniformly distributed, the parameter a represents the lower limit of the uniform distribution, and the parameter b represents the upper limit. If the random number production model is a Gaussian model, the parameter a represents the mean and the parameter b represents the equation. Parameter 5 is valid only when the random number generation method is evenly distributed, indicating whether the generated data is to cover the entire range (not used, so it has not been carefully studied). In addition, it should be noted that the matrix mat used to store random numbers can be multi-dimensional or multi-channel. Currently, at most, only four channels can be supported. Void randShuffle(InputOutputArray dst, double iterFactor=1., RNG* rng=0 ) This function means that the data in the dst of the 1D array is randomly shuffled. The random scrambling method is determined by the random number generator rng. iterFactor is a factor that randomly scrambles the logarithm of the data. The total number of logarithms of data to be shuffled is: dst.rows*dst.cols*iterFactor, so if it is 0, there is no disruption of the data. Class TermCriteria TermCriteria generally represents the termination condition of the iteration. If it is CV_TERMCRIT_ITER, it uses the maximum number of iterations as the termination condition. If it is CV_TERMCRIT_EPS, it uses the precision as the iteration condition. If it is CV_TERMCRIT_ITER+CV_TERMCRIT_EPS, it uses the maximum number of iterations or precision as the iteration condition. The conditions are satisfied first. Double kmeans(InputArray data, int K, InputOutputArray bestLabels, TermCriteria criteria, int attempts, int flags, OutputArray centers=noArray() ) This function is a kmeans clustering algorithm implementation function. The parameter data represents the original data set to be clustered, one row represents a data sample, each column of each sample is an attribute, the parameter k represents the number of clusters to be clustered, and the parameter bestLabels represents the label of each sample's class. , is an integer, starting with zero index integers; argument criteria represents the algorithm iterative termination conditions; parameters attempts represents the number of kmeans to run, the best clustering of the results for the final cluster, with the next parameter Flages to use; parameter flags represents the cluster initialization conditions. There are three cases of its value, if it is KEANANS_RANDOM_CENTERS, it means to select the initialization center point randomly, if it is KMEANS_PP_CENTERS, it means to use an algorithm to determine the initial clustering point; if KEANANS_USE_INITIAL_LABELS, it means to use the user-defined The initial point, but if attempts at this time is greater than 1, then the cluster initial points still use a random way; the parameters centers represent the clustered center point storage matrix. This function returns the compactness of the clustering result. Its calculation formula is: Note one point: This is where I don't understand myself: fill(InputOutputArray mat, int distType, InputArray a, InputArray b, bool saturateRange=false ) Here InputArray a, InputArray b------>>> use Scalar (center.x, center.y, 0, 0), Scalar (img.cols*0.05, img.rows*0.05, 0, 0) to replace To check the manual: InputArray this interface class can be Mat, Mat_ Specifically defined one: InputArray test = Scalar (1,1); this is possible, not to define Mat, Vector does not work, this really do not know what reason, have time to see the use of source a, b. //----The following definitions are all wrong. The results of the operation are not correct. The reason is temporarily unknown. Mat a = (Mat_ Mat b = (Mat_ InputArray a1 = Scalar(center.x, center.y); InputArray b1 = Scalar(img.cols*0.05, img.rows*0.05); Mat a2 = a1.getMat(); Mat b2 = b1.getMat(); Mat c(1, 2, CV_8UC1); c = Scalar(center.x, center.y); Mat c1(1, 2, CV_8UC1); C1 = Scalar(img.cols*0.05, img.rows*0.05); Rng.fill(pointChunk, RNG::NORMAL, a, b, 0); Note two: The input of the kmeans() function only accepts data0.dims <= 2 && type == CV_32F && K > 0 , The first dims generally do not cross the border (3D does not work) The second parameter CV_32F == float, do not bring CV_8U == uchar The third parameter needless to say, the type of setting is definitely greater than 0 Note three points: The sample data, labels, and center point storage of the k-means function in opencv: #include #include Using namespace cv; Using namespace std; Int main(int argc, char** argv) { Mat img(500, 500, CV_8UC3); RNG rng (12345); Const int Max_nCluster = 5; Scalar colorTab[] = { Scalar (0, 0, 255), Scalar(0, 255, 0), Scalar(255, 0, 0), Scalar(0, 255, 255), Scalar(255, 0, 255) }; //InputArray a = Scalar(1,1); Int numCluster = rng.uniform(2, Max_nCluster + 1);//random class number Int sampleCount = rng.uniform(5, 1000);//sample points Mat matPoints(sampleCount, 1, CV_32FC2);//sample point matrix: sampleCount X 2 Mat labels; Mat centers; // Generate a random number For (int k = 0; k < numCluster; k++) { Point center;//randomly generated center point Center.x = rng.uniform(0, img.cols); Center.y = rng.uniform(0, img.rows); Mat pointChunk = matPoints.rowRange( k*sampleCount / numCluster, (k + 1)*sampleCount / numCluster); //-----I don't understand the meaning of this sentence. It doesn't make sense! /*Mat pointChunk = matPoints.rowRange(k*sampleCount / numCluster, k == numCluster - 1 ? sampleCount : (k + 1)*sampleCount / numCluster);*/ //----- Gaussian random Gaussian distribution Rng.fill(pointChunk, RNG::NORMAL, Scalar(center.x, center.y, 0, 0), Scalar(img.cols*0.05, img.rows*0.05, 0, 0)); } randShuffle(matPoints, 1, &rng);//Disrupt Gaussian generated data point order // Use KMeans Kmeans(matPoints, numCluster, labels, TermCriteria(:TermCriteria::EPS + TermCriteria::COUNT, 10, 0.1), 3, KMEANS_PP_CENTERS, centers); // Display categories with different colors Img = Scalar::all(255); For (int i = 0; i < sampleCount; i++) { Int index = labels.at Point p = matPoints.at Circle(img, p, 2, colorTab[index], -1, 8); } // draw the circle at the center of each cluster For (int i = 0; i < centers.rows; i++) { Int x = centers.at Int y = centers.at Printf("cx= %d, cy=%d", x, y); Circle(img, Point(x, y), 40, colorTab[i], 1, LINE_AA); } Imshow("KMeans-Data-Demo", img); waitKey(0); Return 0; } Classification code: #include #include Using namespace cv; Using namespace std; RNG rng (12345); Const int Max_nCluster = 5; Int main(int argc, char** argv) { //Mat img(500, 500, CV_8UC3); Mat inputImage = imread("1.jpg"); Assert(!inputImage.data); Scalar colorTab[] = { Scalar (0, 0, 255), Scalar(0, 255, 0), Scalar(255, 0, 0), Scalar(0, 255, 255), Scalar(255, 0, 255) }; Mat matData = Mat::zeros(Size(inputImage.channels(), inputImage.rows*inputImage.cols), CV_32FC1); Int ncluster = 5; //rng.uniform(2, Max_nCluster + 1);//number of clusters Mat label;//cluster tag Mat centers(ncluster, 1, matData.type()); For (size_t i = 0; i < inputImage.rows; i++) // stores the image into a sample container { Uchar* ptr = inputImage.ptr For (size_t j = 0; j < inputImage.cols; j++) { matData.at matData.at matData.at } } Mat result = Mat::zeros(inputImage.size(), inputImage.type()); TermCriteria criteria = TermCriteria(TermCriteria::EPS + TermCriteria::COUNT, 20, 0.1); Kmeans(matData, ncluster, label, criteria, 3, KMEANS_PP_CENTERS, centers); For (size_t i = 0; i < inputImage.rows; i++) { For (size_t j = 0; j < inputImage.cols; j ++) { Int index = label.at Result.at Result.at Result.at } } Imshow("12", result); waitKey(0); Return 0; } 1200 puffs disposable vape pen are so convenient, portable, and small volume, you just need to take them 1200 puff disposable vape,1200 puffs vape kit,disposable vape 1200 puffs,1200 puffs vape stick,1200 puffs vape pen Ningbo Autrends International Trade Co.,Ltd. , https://www.mosvape.com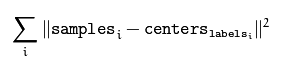



out of your pocket and take a puff, feel the cloud of smoke, and the fragrance of fruit surrounding you. It's so great.
We are China's leading manufacturer and supplier of disposable vape puff bars,1200 puff disposable vape, 1200 puffs vape kit,
disposable vape 1200 puffs,1200 puffs vape stick,1200 puffs vape pen, and e-cigarette kit, and we specialize in Disposable Vapes,
e-cigarette vape pens, e-cigarette kits, etc.